
Symmetry can be very useful to help determine the location of the centroid of an area. It is often useful for the centroid of the area to be determined in either case. The planar surface (or figure) may represent an actual area (like a tributary floor area or the cross-section of a beam) or a figurative diagram (like a load or a bending moment diagram). The centroid of a two dimensional surface (such as the cross-section of a structural shape) is a point that corresponds to the center of gravity of a very thin homogeneous plate of the same area and shape. The Beams Shown are a Wood and Steel Beams

We will limit our application of the Moment of Inertia as it applies to Structural Components identified here. The farther out the object's mass is, the more rotational inertia the object has, and the more force is required to change its rotation rate.

Therefore, it encompasses not just how much mass the object has overall, but how far each bit of mass is from the axis. The moment of inertia of an object about a given axis describes how difficult it is to change its angular motion about that axis. The symbol I and sometimes J are usually used to refer to the moment of inertia or polar moment of inertia. The moment of inertia plays much the same role in rotational dynamics as mass does in linear dynamics, describing the relationship between angular momentum and angular velocity, torque and angular acceleration, and several other quantities. It is the inertia of a rotating body with respect to its rotation. In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, (SI units kg m 2) is a measure of an object's resistance to changes to its rotation. (b) 9.(d) 10.(Moment of Inertia - TotalConstructionHelp) Question.10. The moment of inertia of a circular section about an axis perpendicular to the section isġ. Question.9. The moment of inertia of a circular section of base ‘b’ and height ‘h’ about an axis passing through its vertex and parallel to base is Question.8. The moment of inertia of a body is always minimum with respect to its The moment of inertia of a triangular section of base ‘b’ and height ‘h’ about an axis passing through its base is ………. times the moment of inertia about an axis passing through its C.G. Question.6. The polar moment of inertia of a circular section is about The moment of inertia of a triangular section of base ‘b’ and height’h’ about an axis passing through its C.G. The moment of inertia of a circular section of diameter ‘d’ about its centroidal axis is given by The moment of inertia of a rectangle base ‘b’ and depth ‘d’ about the base will be Question.2. The unit of moment of inertia is
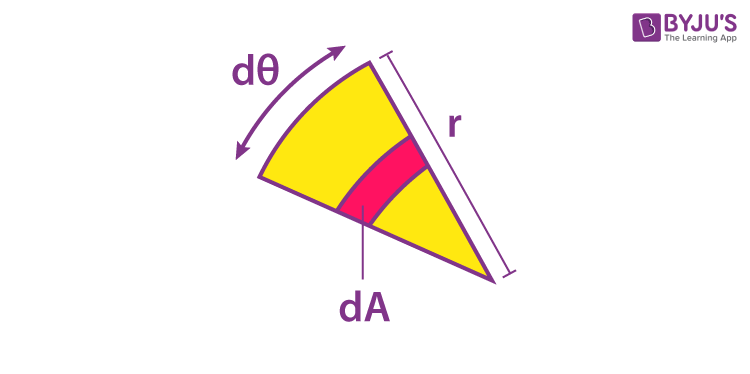
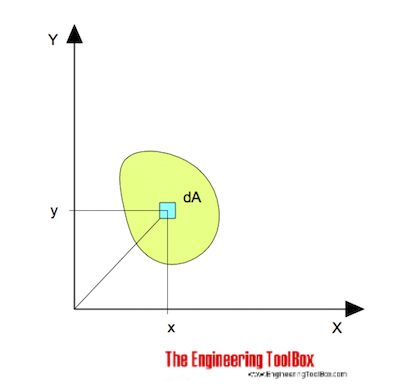
(d) Depends upon the shape of the section (c) Depends upon the dimensions of the section


 0 kommentar(er)
0 kommentar(er)
